Applying Signal Statistical Analysis To TEOAE Measurements

Armin Giebel

a.giebel@lrz.fh-muenchen.de

INTRODUCTION

During the early years of clinical application of otoacoustic emissions, the signal evaluation was primarily based on an expert's decision regarding the waveforms of averaged signals. Mathematical indications, yielded by clinical standard devices, were commonly regarded as additional information only. In succeeding years, however, as a consequence of general hearing screening programs, automated evaluation methods have more and more frequently replaced the judgement of an experienced observer. As a result, many different propositions were made concerning the threshold values for signal statistical evaluation in an effort to make an expert's decision virtually unnecessary. These tendencies require a critical review regarding the validity and reliability of commonly used objective evaluation criteria for otoacoustic emissions.

In the case of transiently evoked emissions, commercially available systems yield mainly two statistical measures:

• The signal correlation of two different averaging buffers (a(t) and b(t)). This correlation is calculated for the unfiltered signal as well as for band-pass filtered signals around different frequencies.
  
  
• The power ratio between the sum (a(t)+b(t)) and the difference (a(t)-b(t)) of the two buffers, mostly denoted as "signal-to-noise ratio (SNR)". This term is somewhat misleading because the buffer sum does not contain the evoked signal alone (if present), but also the averaged noise background.

It is well-known that this kind of signal analysis is not non-parametric. Appropriate values which could effectively discriminate between signals containing an evoked response and those with pure noise cannot be defined without knowing the degrees of freedom of the underlying signals. Thus, the bandwidth determines the statistical distribution of the "just by chance" correlation of two noise signals. The lower the bandwidth, the broader the corresponding distribution. Fig. 1 demonstrates this relationship for three different spectral distributions of noise.


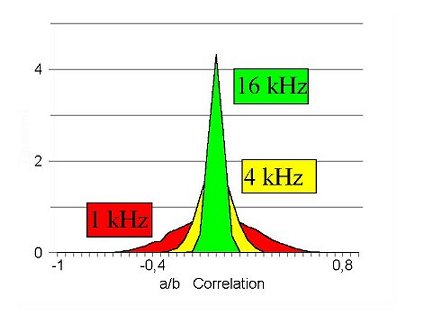
Figure 1: Correlation distribution for pure noise signals with different bandwidths

The objective of this paper is to determine the sensitivity, specificity and time consumption of signal evaluation methods under different environmental conditions. This is accomplished by means of repeated measurement simulations using real signals.

METHODS

Since it is not possible to repeat a physiological test without changing the environmental influences, the measurement procedure was simulated 200 times for the same noise spectra. This was done with and without adding evoked emission signals. Thus it was possible to make statements about different aspects of the tests.

• With an evoked signal being present, the distribution of test times to achieve a certain criterion could be determined, as well as the specificity of the test, which is limited by the percentage of "false fails" (type II errors) for a given number of sweeps
  
  
• Without an evoked signal (pure noise condition), the sensitivity of the test was estimated, that is determined by the percentage of "false passes" (type I errors)
  
  

Three signal statistical approaches were investigated:

1. Buffer correlation between a(t) and b(t) Pass criterion: correlation coefficient above 60 and 75%, respectively;

2. Buffer + / - difference: this term denotes the ratio between the spectral power of the buffer sum (a(t) + b(t)) and their difference (a(t)-b(t)). Pass criterion: difference ratio above 6 and 10 dB, respectively.

3. Binomial statistical test: the binomial average was calculated for each phase locked point within the evaluation interval. Pass criterion: four pairs of positive and negative peaks with a peak-to-peak amplitude of at least 6*SQRT(n), where (n) denotes the number of sweeps applied so far.

The investigation measured for different real emission signals and noise distributions. For each simulation procedure, the noise was added to the phase-locked signal by keeping the noise spectrum constant and varying the phases randomly. If the pass criterion was achieved, the result was registered as "pass" together with the number of sweeps necessary to achieve the "pass". The next run was subsequently started. If the criterion was not achieved after 1000 sweeps, the result was registered as "fail". In order to obtain statistical data, 200 runs were measured for each condition.

RESULTS

Because of the large variety of possible conditions, only some typical results can be presented for common measurement conditions.Fig. 2 demonstrates the results of measurement 200 simulation runs for octave band (Fig. 2a) as well as for tertiary band (Fig. 2b) noise conditions. The x-axis denotes the number of sweeps that were necessary to achieve the required criterion. The y-axis denotes the corresponding frequency of achievement. If the pass criterion was not fulfilled after 1024 sweeps, the evaluation was stopped with a „fail" result. The signal-to-noise ratio was set -20 dB. Sensitivity (percentage of „fail" results in the pure noise condition) , specificity (percentage of passes in the signal+noise condition) and mean relative time consumption for different situations are summarized in Table I.


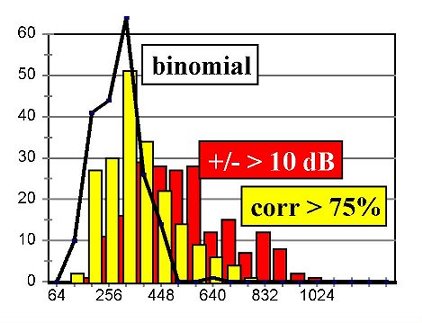
Figure 2: Time consumption distributions for different signal analysis methods a. octave band noise


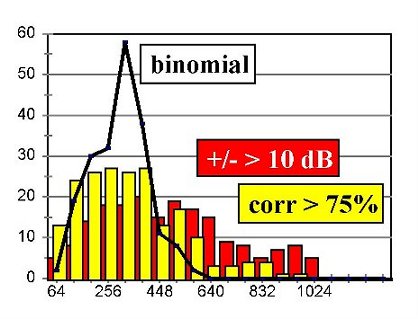
Figure 2: Time consumption distributions for different signal analysis methods b. tertiary band noise

sensitivity / specificity	corr > 60%	+/- > 6dB	corr >75%	+/- >10dB	Binomial
octave band [%]	98/100	99/100	100/100	100/99	100/100
tertiary band [%	74/100	80/100	90/100	98/96	100/100
time consumption
broad band [rel]	70	71	113	175	95
narrow band [rel]	53	63	108	176	93

Table 1: Comparison of validity and time outcomes different pass-criteria in different noise situations. +/- denotes the spectral power ratio between averaging buffers sum and difference.

DISCUSSION

The results show that conventional TEOAE assessment by buffer correlation and +/- difference criteria may work sufficiently well for flat broad band noise spectra. However, if the noise spectrum contains "peaks", which is common in real measurements, the validity decreases. This is especially true when the signal is additionally filtered in order to gain information about specific frequency bands. Moreover, the time to obtain a result increases and becomes more unpredictable.

CONCLUSIONS

Automated TEOAE signal evaluation methods should be applicable for screening even under non-optimal conditions. Therefore, robust algorithms high validity and reliability witthat are virtually non-parametric have to be introduced in order to replace the conventional signal analysis. A procedure based on binomial statistics is much less dependent on the environmental noise conditions, in spite of the fact that it is not completely non-parametric, too, because of coupling effects between neighbouring points.

The study was carried out under the assumption of constant noise. Further investigations should consider the influence of varying noise during the measurement.